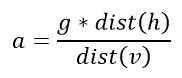INTRODUCTION
In the CB400 thread on Netrider, Positron007 speculated that the CB400 (which accelerates really quickly to 70kph) accelerates as fast as a 600cc sportsbike, at least up to the first gearchange.
He speculated that the limiting factor (up to 70km/h) was not the power of the bikes (which are vastly different) but the fact that you’re trying to prevent the bikes from doing a wheelie for this whole time.
So today, I thought I’d use my nerd powers for good instead of evil, and take a crack at explaining a wheelie formulaically. I couldn’t really find anything explaining the physics behind a wheelie on Google, so I thought I’d have a crack at it myself.
Disclaimer: May be wrong.
TL;DR: Positron is right, 600cc bikes don’t really accelerate faster (to 70kph) than the CB400.

 

ASSUMPTIONS
Assumption 1 – That both the CB400 and the 600cc sportsbike (which I’ll call the CBR600RR from now on) are both at their ‘liftoff point’ for the whole drag-race (which will be up to 70km/h, after which the CB400 is not capable of wheelie-ing).
Assumption 2 – The CB400 weighs 270kg fully laden with 76kg rider, and it’s COG (with rider) lies 600mm and 500mm from the rear axle.
Assumption 3 – The CBR600RR weighs 273kg fully laden with 76kg rider, and it’s COG (with rider) lies 650mm and 550mm from the rear axle.
Assumption 4 – Gravity is 9.81 m/s2

 

DISCUSSION
Why is the liftoff point important? A bike is accelerating at its fastest when the front wheel is at the point of becoming weightless. If the bike is accelerating any faster than this, then the front wheel will continue to lift off the ground, until the rider is on his back. (See endless YouTube videos to see this effect in action).
At liftoff point, both the liftoff and the gravitational turning moments are equal. What do I mean by this?

To describe this as a formula:

Moment (downwards) = Moment (upwards)

Aside:
I don’t think that this formula applies to drag-cars and other very-high performance vehicles. The principles do apply, but they also have some massive lifting forces created by the torquing action on their drivetrain. Bikes do not have torque-induced lift, especially at the low-power levels we’re looking at here.

The turning moment is the force multiplied by the perpendicular distance to the turning point, and can be described by the formula:

 Mt = F * D

To show the turning moments visually:

Horizontal Turning Moment

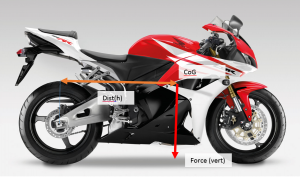
Vertical Turning Moment

Force is described by the formula

 F = m * a

So, to combine all these equations

Solving for acceleration provides:

This is quite an interesting result, as the mass cancels out of both sides. Ergo, the mass of the bike has nothing to do with the bike’s ability to keep the front end off the ground. (Naturally, the bike’s mass will have a lot to do in limiting the amount of acceleration available to the bike.)

So it all comes down to the D(h) against D(v) ratio. In retrospect, this makes sense, as it is well-known that an adequately powerful cruiser can out-accelerate a sportsbike, due to its low COG and long wheelbase (more forward COG).

 

CONCLUSION

So comparing the CB400 against the CB600RR:

 

So the CB400 will actually out-accelerate the CBR, though there is not much in it. These accelerations will mean that the bikes will do 0-70km/h in 1.7 seconds. NOTE: The numbers for the vertical and horizontal distances are pure guesswork. Any assistance to provide real numbers would be greatly appreciated.

 

In Summary:

• The maximum acceleration threshold for a bike is limited by its turning moment.
  • At any point below this threshold, acceleration will be limited by other factors, such as power, gearing, weight, etc.
  • The turning moment is a factor of the height and distance of the COG of the Bike (and rider) from the rear-axle.
  • Any two bikes which have sufficiently similar COG distances will have the same maximum acceleration threshold.